Potential field based planner
One approach is to treat the robot's configuration as a point (usually electron) in a potential field that combines attraction to the goal, and repulsion from obstacles. The resulting trajectory is output as the path. This approach has advantages in that the trajectory is produced with little computation. However, they can become trapped in local minima of the potential field, and fail to find a path. The Artificial potential fields can be achieved by direct equation similar to electrostatic potential fields or can be drive by set of linguistic rules
Input: 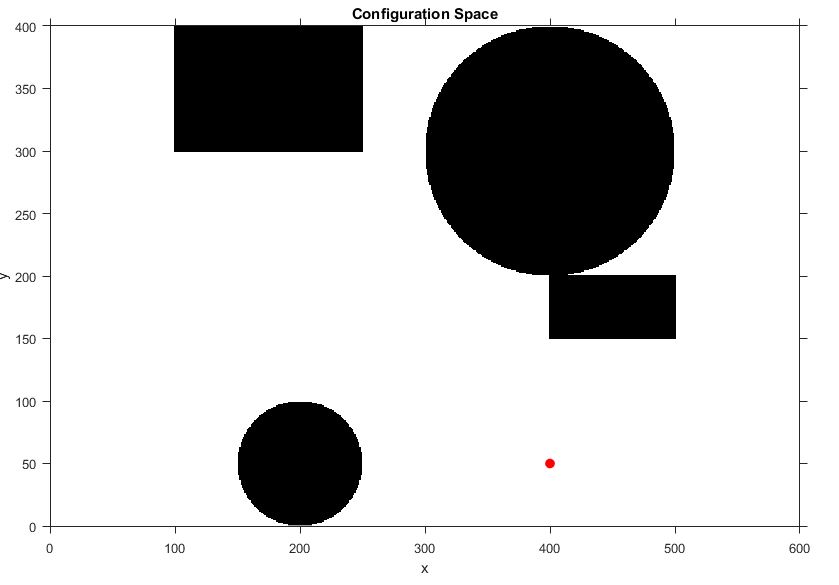 ---->
---->
Output: 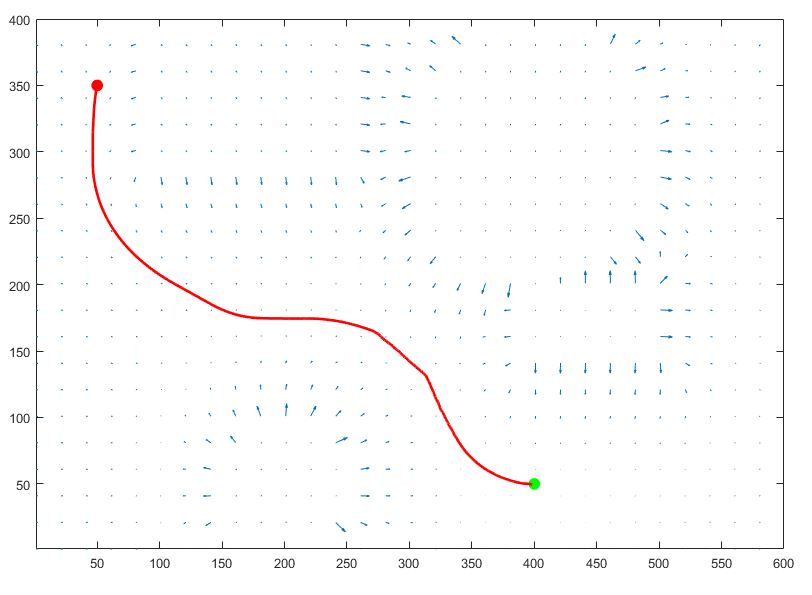
Potentials: 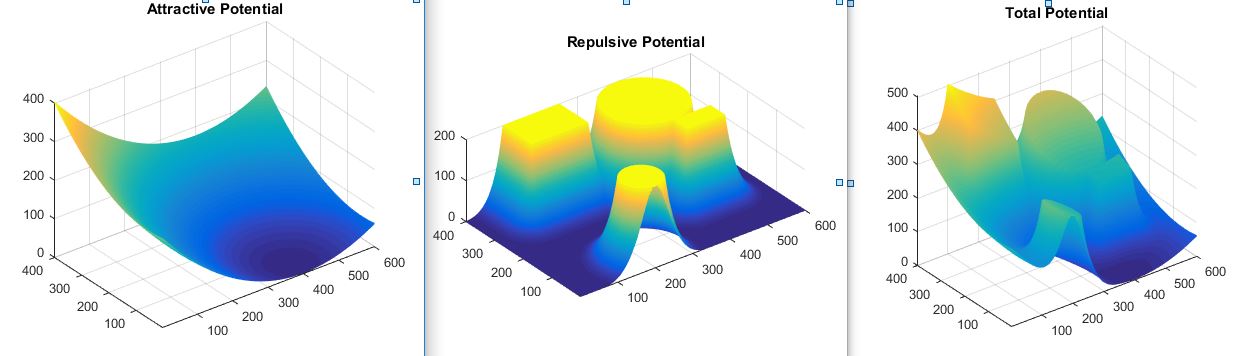
%
% PotentialFieldScript.m
%
close all, clear all
%% Generate some points
nrows = 400;
ncols = 600;
obstacle = false(nrows, ncols);
[x, y] = meshgrid (1:ncols, 1:nrows);
%% Generate some obstacle
obstacle (300:end, 100:250) = true;
obstacle (150:200, 400:500) = true;
t = ((x - 200).^2 + (y - 50).^2) < 50^2;
obstacle(t) = true;
t = ((x - 400).^2 + (y - 300).^2) < 100^2;
obstacle(t) = true;
%% Compute distance transform
d = bwdist(obstacle);
% Rescale and transform distances
d2 = (d/100) + 1;
d0 = 2;
nu = 800;
repulsive = nu*((1./d2 - 1/d0).^2);
repulsive (d2 > d0) = 0;
%% Display repulsive potential
figure(1);
m = mesh (repulsive);
m.FaceLighting = 'phong';
axis equal;
title ('Repulsive Potential');
%% Compute attractive force
goal = [400, 50];
xi = 1/700;
attractive = xi * ( (x - goal(1)).^2 + (y - goal(2)).^2 );
figure(2);
m = mesh (attractive);
m.FaceLighting = 'phong';
axis equal;
title ('Attractive Potential');
%% Display 2D configuration space
figure(3);
imshow(~obstacle);
hold on;
plot (goal(1), goal(2), 'r.', 'MarkerSize', 25);
hold off;
axis ([0 ncols 0 nrows]);
axis xy;
axis on;
xlabel ('x');
ylabel ('y');
title ('Configuration Space');
%% Combine terms
f = attractive + repulsive;
figure(4);
m = mesh (f);
m.FaceLighting = 'phong';
axis equal;
title ('Total Potential');
%% Plan route
start = [50, 350];
route = GradientBasedPlanner (f, start, goal, 1000);
%% Plot the energy surface
figure(5);
m = mesh (f);
axis equal;
%% Plot ball sliding down hill
[sx, sy, sz] = sphere(20);
scale = 20;
sx = scale*sx;
sy = scale*sy;
sz = scale*(sz+1);
hold on;
p = mesh(sx, sy, sz);
p.FaceColor = 'red';
p.EdgeColor = 'none';
p.FaceLighting = 'phong';
hold off;
for i = 1:size(route,1)
P = round(route(i,:));
z = f(P(2), P(1));
p.XData = sx + P(1);
p.YData = sy + P(2);
p.ZData = sz + f(P(2), P(1));
drawnow;
drawnow;
end
%% quiver plot
[gx, gy] = gradient (-f);
skip = 20;
figure(6);
xidx = 1:skip:ncols;
yidx = 1:skip:nrows;
quiver (x(yidx,xidx), y(yidx,xidx), gx(yidx,xidx), gy(yidx,xidx), 0.4);
axis ([1 ncols 1 nrows]);
hold on;
ps = plot(start(1), start(2), 'r.', 'MarkerSize', 30);
pg = plot(goal(1), goal(2), 'g.', 'MarkerSize', 30);
p3 = plot (route(:,1), route(:,2), 'r', 'LineWidth', 2);
function route = GradientBasedPlanner (f, start_coords, end_coords, max_its)
% GradientBasedPlanner : This function plans a path through a 2D
% environment from a start to a destination based on the gradient of the
% function f which is passed in as a 2D array. The two arguments
% start_coords and end_coords denote the coordinates of the start and end
% positions respectively in the array while max_its indicates an upper
% bound on the number of iterations that the system can use before giving
% up.
% The output, route, is an array with 2 columns and n rows where the rows
% correspond to the coordinates of the robot as it moves along the route.
% The first column corresponds to the x coordinate and the second to the y coordinate
[gx, gy] = gradient (-f);
%%% All of your code should be between the two lines of stars.
% *******************************************************************
route = start_coords;
pos = start_coords;
running = true;
i = 0;
%route = [start_coords(1), start_coords(2)];
while running
if (i == max_its) || (norm(end_coords - pos) < 2)
running = false;
break;
end
% while (i < max_its) && (f(pos(2),pos(1)) > )
Delta = [ gx( round(pos(2)), round(pos(1)) ), ....
gy( round(pos(2)), round(pos(1)) )];
pos = pos + Delta/norm(Delta);
route = [route; pos];
i = i + 0.5;
end
% *******************************************************************
end
One approach is to treat the robot's configuration as a point (usually electron) in a potential field that combines attraction to the goal, and repulsion from obstacles. The resulting trajectory is output as the path. This approach has advantages in that the trajectory is produced with little computation. However, they can become trapped in local minima of the potential field, and fail to find a path. The Artificial potential fields can be achieved by direct equation similar to electrostatic potential fields or can be drive by set of linguistic rules
Input:Output:
Potentials:
%
% PotentialFieldScript.m
%
close all, clear all
%% Generate some points
nrows = 400;
ncols = 600;
obstacle = false(nrows, ncols);
[x, y] = meshgrid (1:ncols, 1:nrows);
%% Generate some obstacle
obstacle (300:end, 100:250) = true;
obstacle (150:200, 400:500) = true;
t = ((x - 200).^2 + (y - 50).^2) < 50^2;
obstacle(t) = true;
t = ((x - 400).^2 + (y - 300).^2) < 100^2;
obstacle(t) = true;
%% Compute distance transform
d = bwdist(obstacle);
% Rescale and transform distances
d2 = (d/100) + 1;
d0 = 2;
nu = 800;
repulsive = nu*((1./d2 - 1/d0).^2);
repulsive (d2 > d0) = 0;
%% Display repulsive potential
figure(1);
m = mesh (repulsive);
m.FaceLighting = 'phong';
axis equal;
title ('Repulsive Potential');
%% Compute attractive force
goal = [400, 50];
xi = 1/700;
attractive = xi * ( (x - goal(1)).^2 + (y - goal(2)).^2 );
figure(2);
m = mesh (attractive);
m.FaceLighting = 'phong';
axis equal;
title ('Attractive Potential');
%% Display 2D configuration space
figure(3);
imshow(~obstacle);
hold on;
plot (goal(1), goal(2), 'r.', 'MarkerSize', 25);
hold off;
axis ([0 ncols 0 nrows]);
axis xy;
axis on;
xlabel ('x');
ylabel ('y');
title ('Configuration Space');
%% Combine terms
f = attractive + repulsive;
figure(4);
m = mesh (f);
m.FaceLighting = 'phong';
axis equal;
title ('Total Potential');
%% Plan route
start = [50, 350];
route = GradientBasedPlanner (f, start, goal, 1000);
%% Plot the energy surface
figure(5);
m = mesh (f);
axis equal;
%% Plot ball sliding down hill
[sx, sy, sz] = sphere(20);
scale = 20;
sx = scale*sx;
sy = scale*sy;
sz = scale*(sz+1);
hold on;
p = mesh(sx, sy, sz);
p.FaceColor = 'red';
p.EdgeColor = 'none';
p.FaceLighting = 'phong';
hold off;
for i = 1:size(route,1)
P = round(route(i,:));
z = f(P(2), P(1));
p.XData = sx + P(1);
p.YData = sy + P(2);
p.ZData = sz + f(P(2), P(1));
drawnow;
drawnow;
end
%% quiver plot
[gx, gy] = gradient (-f);
skip = 20;
figure(6);
xidx = 1:skip:ncols;
yidx = 1:skip:nrows;
quiver (x(yidx,xidx), y(yidx,xidx), gx(yidx,xidx), gy(yidx,xidx), 0.4);
axis ([1 ncols 1 nrows]);
hold on;
ps = plot(start(1), start(2), 'r.', 'MarkerSize', 30);
pg = plot(goal(1), goal(2), 'g.', 'MarkerSize', 30);
p3 = plot (route(:,1), route(:,2), 'r', 'LineWidth', 2);
function route = GradientBasedPlanner (f, start_coords, end_coords, max_its)
% GradientBasedPlanner : This function plans a path through a 2D
% environment from a start to a destination based on the gradient of the
% function f which is passed in as a 2D array. The two arguments
% start_coords and end_coords denote the coordinates of the start and end
% positions respectively in the array while max_its indicates an upper
% bound on the number of iterations that the system can use before giving
% up.
% The output, route, is an array with 2 columns and n rows where the rows
% correspond to the coordinates of the robot as it moves along the route.
% The first column corresponds to the x coordinate and the second to the y coordinate
[gx, gy] = gradient (-f);
%%% All of your code should be between the two lines of stars.
% *******************************************************************
route = start_coords;
pos = start_coords;
running = true;
i = 0;
%route = [start_coords(1), start_coords(2)];
while running
if (i == max_its) || (norm(end_coords - pos) < 2)
running = false;
break;
end
% while (i < max_its) && (f(pos(2),pos(1)) > )
Delta = [ gx( round(pos(2)), round(pos(1)) ), ....
gy( round(pos(2)), round(pos(1)) )];
pos = pos + Delta/norm(Delta);
route = [route; pos];
i = i + 0.5;
end
% *******************************************************************
end